What is a Truth Table?
Ever stared at a logic problem and felt completely lost? You're not alone. A truth table is your roadmap through the maze of Boolean logic - think of it as a GPS for digital reasoning.
A truth table is a mathematical table that displays all possible input combinations for a logical expression and their corresponding outputs. Imagine you're planning a picnic and need both sunny weather AND a free weekend. A truth table would show you all four possibilities: sunny + free (go!), sunny + busy (stay home), rainy + free (stay home), rainy + busy (definitely stay home).
Quick Insight: Truth tables are everywhere in your daily life. Your smartphone makes millions of these logical decisions every second - from checking if you have both battery power AND network signal before sending a message, to determining if you should get a notification based on your settings.
Core Components of Truth Tables
Input Variables: These represent the conditions entering your logic system. We typically use letters like A, B, C, D. Each variable is binary - it's either True (1) or False (0). No maybe, no sometimes, just yes or no.
Output Column: This shows what happens when you combine all those inputs according to your logical rules. It's like the final answer to your "if this and that, then what?" question.
Systematic Organization: Truth tables list every possible combination in a predictable order. For two variables, you get four rows (00, 01, 10, 11). It's like counting in binary - systematic and complete.
🧮 Try Our Boolean Algebra Calculator
Ready to see truth tables in action? Generate a complete truth table for any expression like (A∧B)∨¬C
Calculate NowWhy Truth Tables Actually Matter
Truth tables aren't just academic exercises - they're the DNA of digital technology. Every app on your phone, every website you visit, every digital device you use relies on the logical principles demonstrated in truth tables.
Visual Clarity: Instead of trying to mentally juggle multiple logical conditions, truth tables lay everything out clearly. You can see exactly how your logic behaves without guesswork.
Error Detection: Ever wonder why your code doesn't work as expected? Truth tables help you spot logical errors before they become bugs. They're like a spell-checker for logic.
Circuit Design: Every computer processor, from your laptop to your car's engine control unit, uses circuits designed using truth table principles.
Real-World Applications That Might Surprise You
Your Car's Safety Systems: Modern vehicles use truth tables to decide when to deploy airbags. They check multiple conditions: collision detected AND seatbelt fastened AND passenger present. Only when all conditions align do the airbags deploy.
Smart Home Security: Your security system uses Boolean logic: motion detected AND alarm armed AND NOT owner's phone detected = trigger alert.
Social Media Algorithms: When Facebook decides what to show in your feed, it uses complex Boolean expressions: friend posted AND you previously liked similar content AND post is recent = show in feed.
Online Shopping: E-commerce sites use truth tables for inventory management: item in stock AND payment verified AND shipping address valid = process order.
How to Read and Create Truth Tables
Creating truth tables might seem intimidating at first, but it's actually like following a recipe. Once you know the steps, you can tackle any logical expression with confidence.
Step-by-Step Truth Table Creation
Step 1: Count Your Variables
Look at your Boolean expression and identify unique variables. In "A ∧ B ∨ C", you have three distinct variables: A, B, and C. Don't count repeated variables twice.
Step 2: Calculate Required Rows
Use the formula 2^n where n is your variable count. Three variables? That's 2³ = 8 rows. Four variables? 2⁴ = 16 rows. The table grows quickly, which is why Boolean simplification becomes important for complex expressions.
Common Mistake Alert: Students often forget that the number of rows doubles with each new variable. Planning ahead saves time and prevents the frustration of realizing you're missing half your truth table.
Step 3: List All Input Combinations Systematically
The secret to accuracy is being systematic. Start with all variables at 0, then count up in binary:
| A | B | C |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| 1 | 1 | 1 |
Step 4: Evaluate Your Expression Row by Row
This is where the magic happens. For each row, substitute the input values into your Boolean expression and calculate the result. Take it slow - rushing here leads to errors that cascade through your entire table.
Step 5: Double-Check Your Work
Professional circuit designers always verify their truth tables. Look for patterns that make sense, check a few rows manually, and use tools to confirm your results.
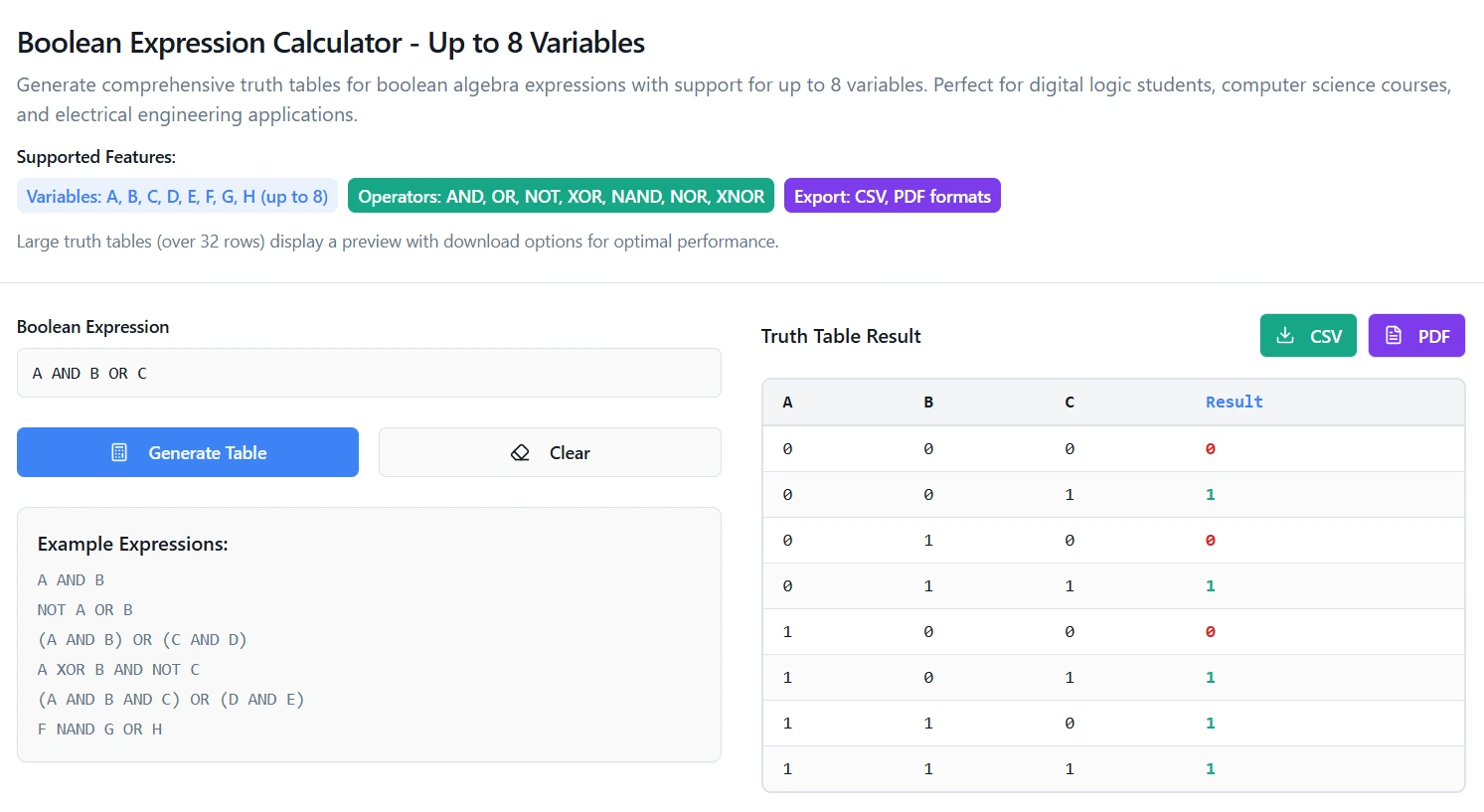
🔍 Verify Your Truth Tables
Unsure about your manual calculations? Our calculator shows step-by-step solutions
Check Your WorkPro Tips for Efficiency
Use Intermediate Columns: For complex expressions like (A∧B)∨(C∧¬D), create separate columns for (A∧B), (C∧¬D), and then the final OR operation. This prevents errors and makes your logic transparent.
Pattern Recognition: After creating several truth tables, you'll start recognizing patterns. An AND gate with any 0 input always outputs 0. An OR gate with any 1 input always outputs 1. These shortcuts speed up your work.
Work in Groups: When possible, evaluate similar expressions together. If you need truth tables for both A∧B and A∨B, create them side by side to see the differences clearly.
Essential Logic Gates and Their Truth Tables
Logic gates are the building blocks of every digital device you use. Understanding their truth tables is like learning the alphabet before reading - fundamental and essential.
AND Gate - The "All or Nothing" Gate
Think of an AND gate like a security vault that needs multiple keys. Only when ALL keys are present (all inputs are True) does the vault open (output becomes True).
| A | B | Output (A ∧ B) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Real-World Example: Your car won't start unless the key is turned AND the brake pedal is pressed. Both conditions must be met - this is AND gate logic in action.
Boolean Expression: Y = A · B or Y = A ∧ B
OR Gate - The "Any Will Do" Gate
An OR gate is like having multiple light switches for the same bulb. Any switch can turn on the light - you don't need all of them.
| A | B | Output (A ∨ B) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Real-World Example: Your phone's emergency alert system triggers if there's a severe weather warning OR an AMBER alert OR a national emergency. Any one condition activates the alert.
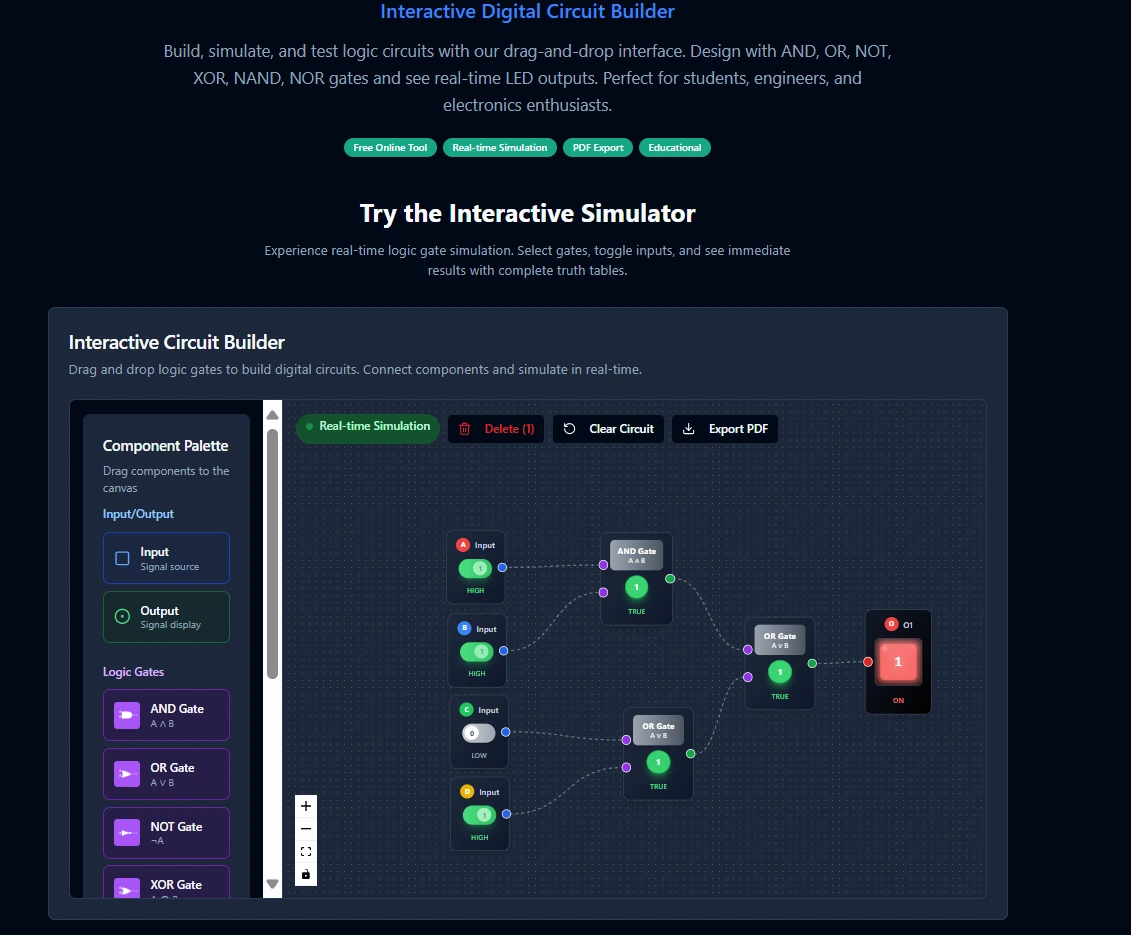
🔗 Build Interactive Circuits
Want to see how gates connect in real circuits? Our logic gate simulator lets you build and test your own designs
Try Circuit SimulatorNOT Gate - The "Opposite Day" Gate
The NOT gate is the simplest but most crucial gate. It always gives you the opposite of what you put in. True becomes False, False becomes True.
| A | Output (¬A) |
|---|---|
| 0 | 1 |
| 1 | 0 |
Real-World Example: A normally-closed fire door that opens when the fire alarm is NOT active. When there's no fire (False), the door stays open (True). When there's a fire (True), the door closes (False).
NAND Gate - The "Universal" Gate
NAND combines AND and NOT - it's the opposite of an AND gate. Here's what makes it special: you can build ANY digital circuit using only NAND gates. That's why it's called a "universal gate."
| A | B | Output (A ↑ B) |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Why It Matters: Computer manufacturers love NAND gates because they can build entire processors using just one type of gate. This simplifies manufacturing and reduces costs.
XOR Gate - The "Different" Gate
XOR (Exclusive OR) outputs True only when inputs are different. It's perfect for detecting changes or differences.
| A | B | Output (A ⊕ B) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Real-World Example: A two-way light switch system in your hallway. Either switch can toggle the light, but the light's state depends on whether the switches are in different positions.
Computer Application: XOR gates are crucial in computer arithmetic and encryption. They're used in adding binary numbers and creating secure communication protocols.
Boolean Algebra Fundamentals
Boolean algebra might sound intimidating, but it's actually simpler than regular algebra. While normal algebra deals with numbers, Boolean algebra only deals with True and False. Think of it as the mathematics of decision-making.
The Basic Laws That Rule Digital Logic
Just like regular algebra has rules (2 + 3 = 3 + 2), Boolean algebra has its own set of laws. Understanding these helps you simplify complex expressions and design efficient circuits.
Identity Laws - The "Obvious" Rules
Real-World Analogy: Adding zero to any number doesn't change it. Similarly, OR-ing with False or AND-ing with True doesn't change your logical value.
Null Laws - The "Override" Rules
Think About It: If you're checking "sunny weather OR guaranteed indoor venue," the guaranteed indoor venue makes the weather irrelevant - you'll have your event regardless.
De Morgan's Laws - The "Flip and Switch" Rules
De Morgan's laws are incredibly powerful for circuit optimization. They let you convert between AND and OR gates, often leading to simpler, cheaper circuit designs.
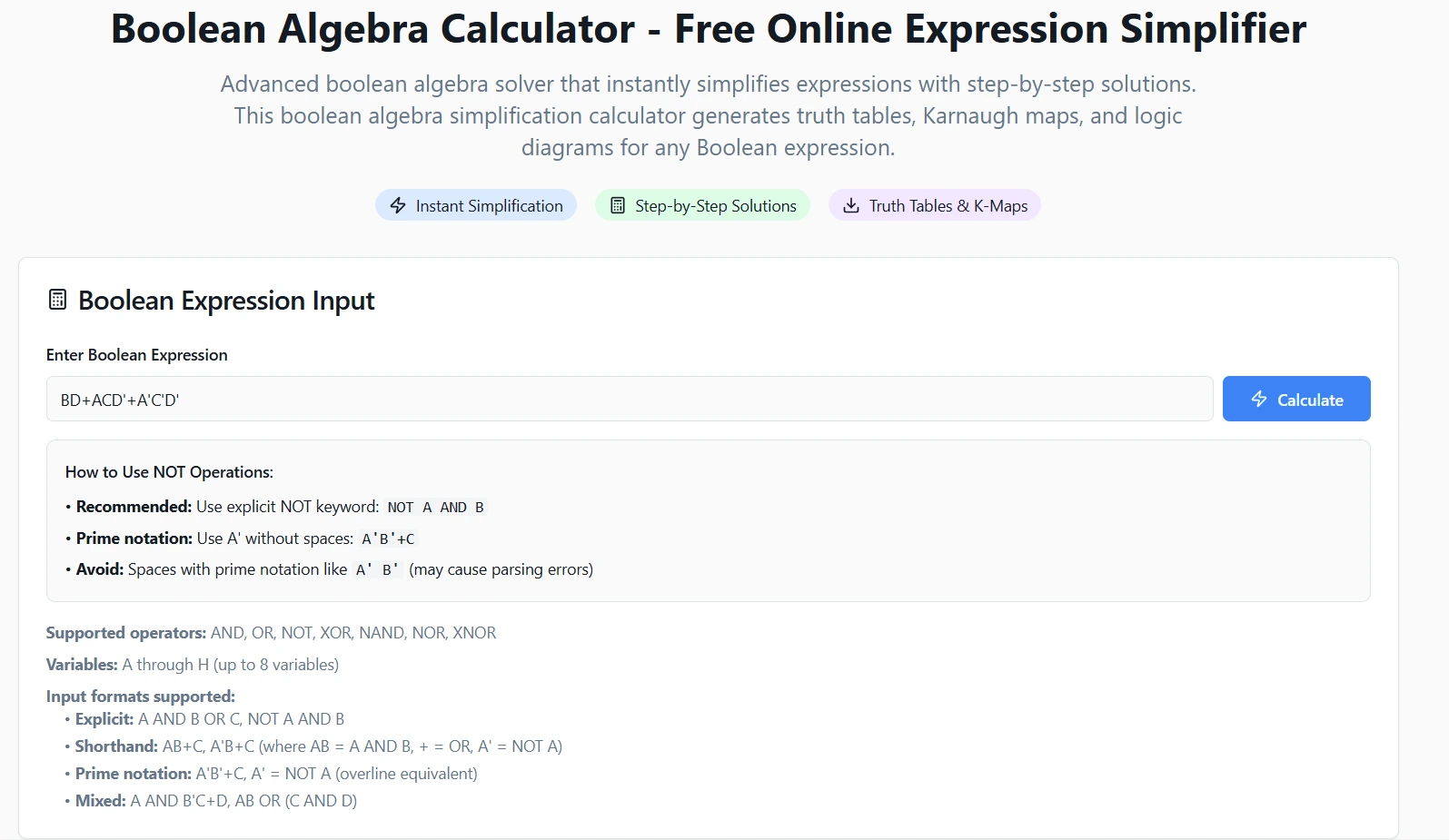
⚡ Simplify Boolean Expressions
See De Morgan's laws and other simplifications in action with step-by-step solutions
Simplify Now
Practical Boolean Simplification
Let's work through a real example that shows why Boolean algebra matters:
Example: Simplifying (A ∧ B) ∨ (A ∧ ¬B)
Step 1: Factor out A → A ∧ (B ∨ ¬B)
Step 2: Apply complement law → A ∧ 1
Step 3: Apply identity law → A
Result: We reduced a complex expression with 4 terms down to just A!
Why This Matters: In circuit design, fewer components mean lower cost, less power consumption, and higher reliability. That simplified expression could save thousands of dollars in a mass-produced device.
Truth Tables for Boolean Verification
Here's a professional tip: every Boolean simplification can be verified using truth tables. Create truth tables for both the original and simplified expressions - if the output columns are identical, your simplification is correct.
This verification process isn't just academic. Circuit designers use truth table verification to catch costly errors before manufacturing begins.
Advanced Truth Table Applications
Once you master basic truth tables, a world of advanced applications opens up. These techniques are used in everything from spacecraft computers to smartphone apps.
Multi-Output Truth Tables
Real systems rarely have just one output. Consider a 7-segment display (like on a digital clock) - it takes a 4-bit input representing digits 0-9 and controls 7 different segments. That's one truth table with 4 inputs and 7 outputs.
Professional Insight: Modern processors have truth tables with dozens of inputs and outputs. The complexity is managed by breaking large problems into smaller, manageable truth tables that work together.
Don't Care Conditions - The Optimization Secret
Sometimes certain input combinations never occur in your system, or their outputs simply don't matter. These "don't care" conditions, marked with "X", are optimization goldmines.
Example: A Binary Coded Decimal (BCD) system only uses combinations 0000 through 1001 to represent digits 0-9. Combinations 1010-1111 never occur, so they're don't cares. This flexibility often allows dramatic circuit simplification.
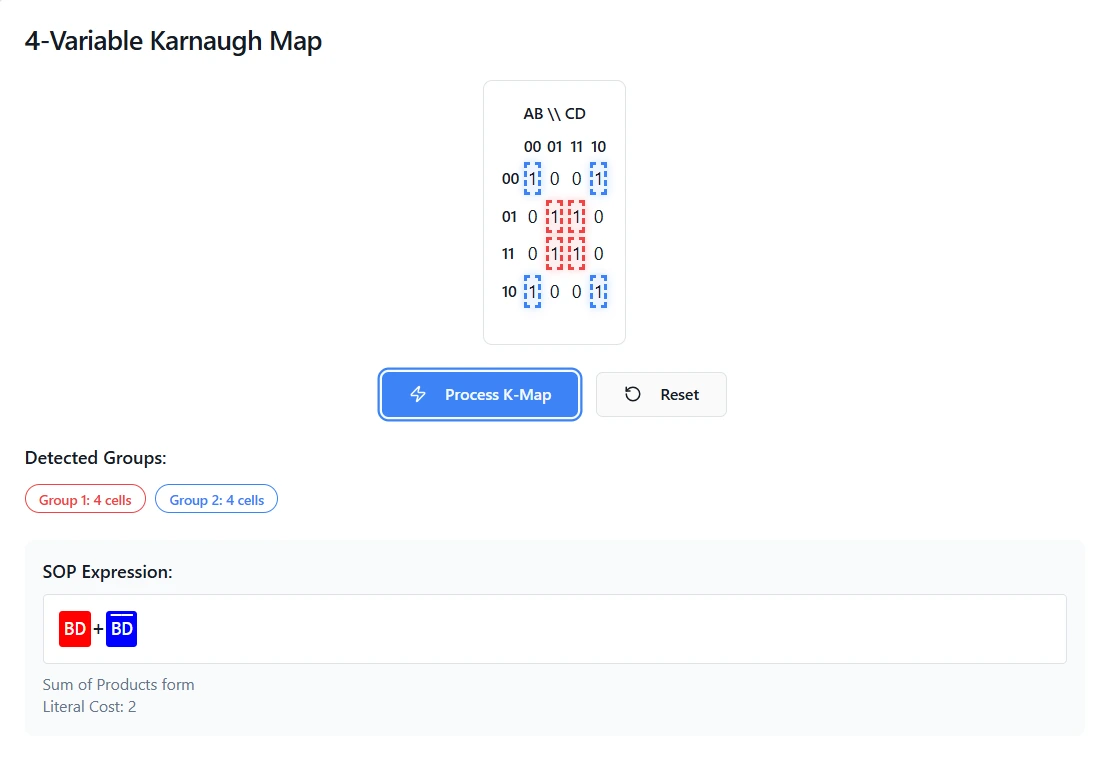
🗺️ Optimize with K-Maps
Don't care conditions shine in Karnaugh Map optimization. See how they simplify complex expressions
Try K-Map SolverState Tables vs Truth Tables
Truth Tables: Handle combinational logic where outputs depend only on current inputs (like logic gates).
State Tables: Handle sequential logic where outputs depend on both current inputs and the system's current state (like flip-flops and counters).
Understanding this distinction is crucial for designing digital systems that remember previous inputs or count sequences.
Timing and Real-World Considerations
Academic truth tables assume instantaneous switching, but real circuits have delays. Professional designers must consider:
- Propagation Delay: Each gate takes time to switch states
- Race Conditions: When signals arrive at different times
- Hazards: Temporary incorrect outputs during transitions
These considerations transform simple truth table logic into robust, reliable digital systems.
Frequently Asked Questions
Master Truth Tables and Advance Your Digital Logic Skills
Truth tables are your foundation for understanding digital logic, computer science, and circuit design. But they're just the beginning of your journey into the fascinating world of Boolean algebra and digital systems.
Now that you understand truth table fundamentals, you're ready to tackle more advanced topics like circuit optimization, sequential logic design, and complex digital system architecture.
🚀 Continue Your Learning Journey
Ready to apply your truth table knowledge? Try our advanced tools and see how professionals solve real-world digital logic problems.
Related Learning Resources
Whether you're solving homework problems, designing digital circuits, or understanding how computers work, truth tables provide the clarity and verification you need for success. Start building truth tables today and unlock the logical thinking that powers our digital world.